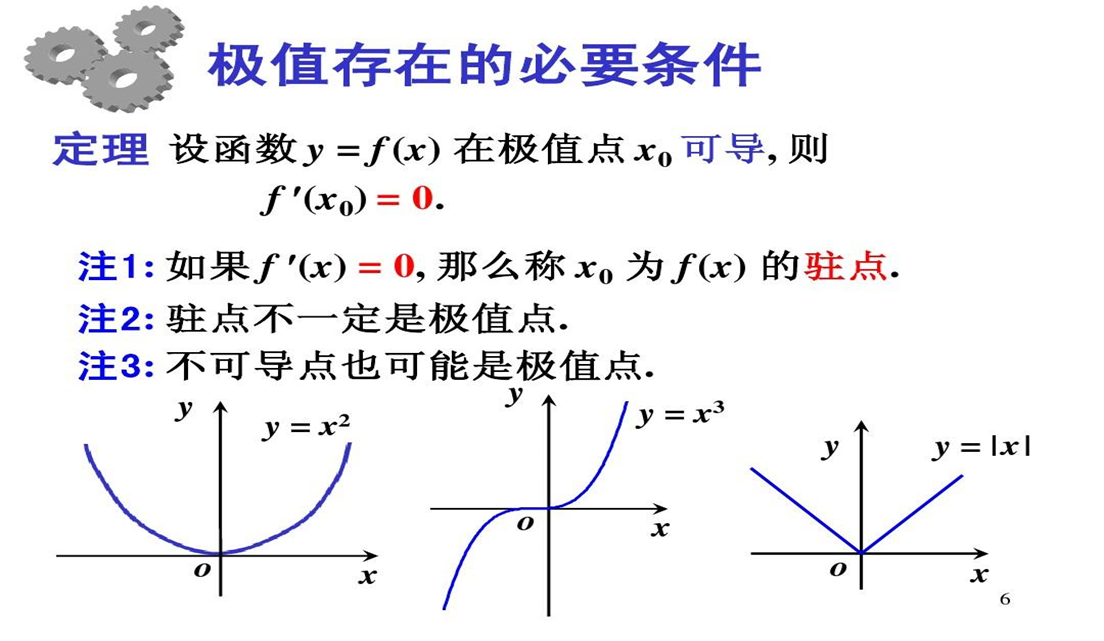
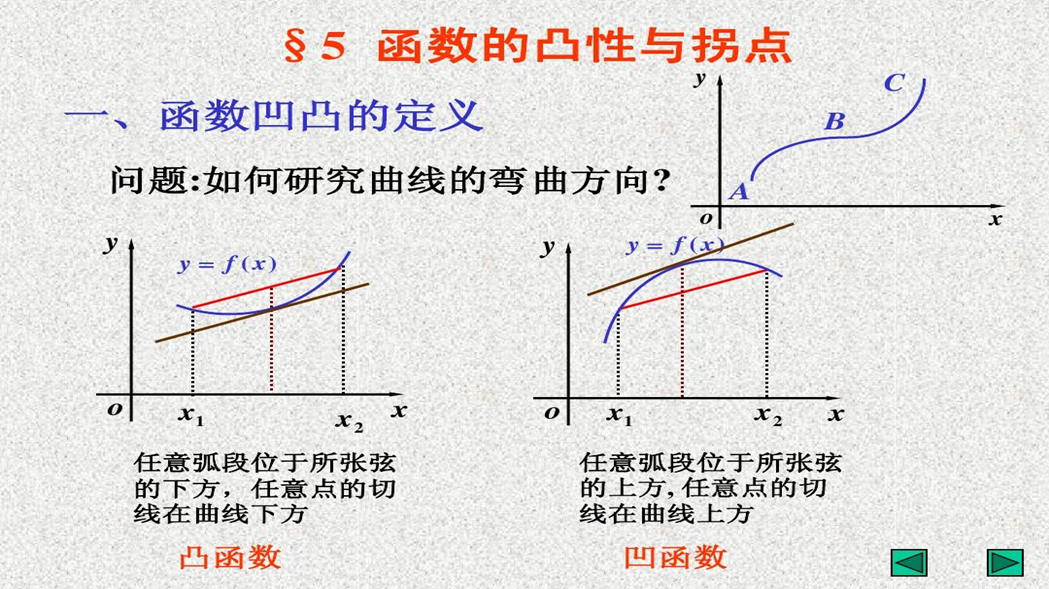
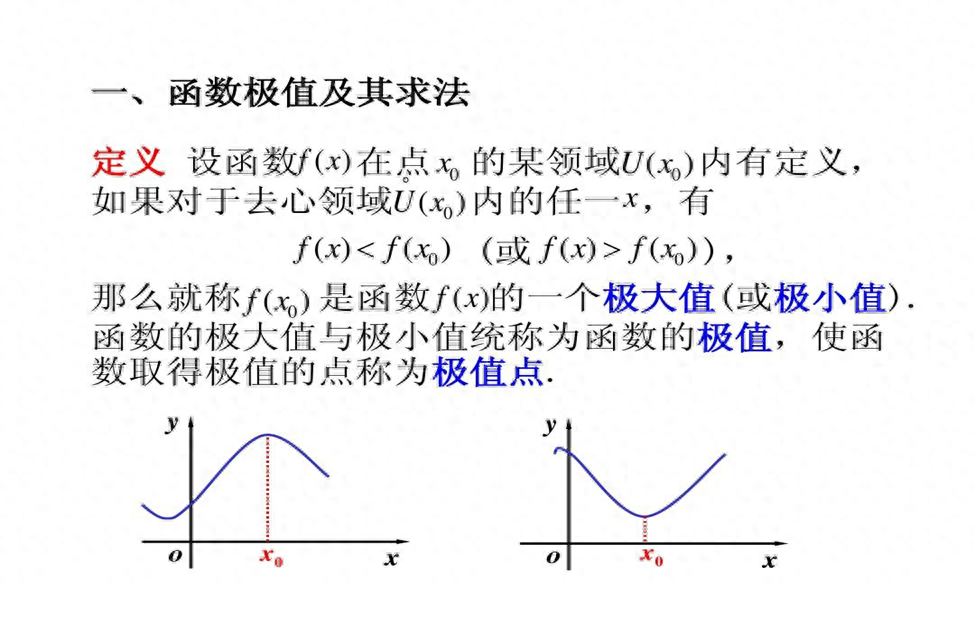
函数的极值和拐点是数学中非常重要的概念,在经济学、生物学、物理学等领域都有广泛的应用。下面我们将详细介绍这两个概念,并探讨如何求函数的极值和拐点。
一、函数的极值
函数的极值是指函数在某一点达到的最大值或最小值。具体来说,如果函数在某一点的导数为零,并且这一点两侧的导数符号相反,那么这个点就是函数的极值点,函数在这个点处的值就是极值。
例如,函数f(x)=x^3在x=0处有极小值f(0)=0,因为f'(0)=0,且在x<0和x>0时,f'(x)均为正值,而在x=0两侧的导数符号相反。
求函数的极值可以通过以下步骤进行:
1. 求出函数的一阶导数;
2. 令一阶导数为零,解出相应的x值;
3. 对于每个极值点,检查其两侧的导数符号是否相反;
4. 确定函数的极值。
二、函数的拐点
函数的拐点是指函数图像在该点处发生弯曲变化的位置。具体来说,如果函数在某一点的二阶导数为零,并且这一点两侧的二阶导数符号相反,那么这个点就是函数的拐点。
例如,函数f(x)=x^4在x=0处有拐点,因为f''(0)=0,且在x<0和x>0时,f''(x)均为正值,而在x=0两侧的二阶导数符号相反。
求函数的拐点可以通过以下步骤进行:
1. 求出函数的二阶导数;
2. 令二阶导数为零,解出相应的x值;
3. 对于每个拐点,检查其两侧的二阶导数符号是否相反;
4. 确定函数的拐点。
三、极值和拐点的应用
函数的极值和拐点在各个领域都有广泛的应用。例如,在经济学的成本收益分析中,极值可以用来确定最大利润或最小成本的点;在生物学的生长曲线中,拐点可以用来描述生长速率的变化等等。
总之,函数的极值和拐点是数学中非常重要的概念,它们在各个领域都有广泛的应用。通过掌握求极值和拐点的步骤和方法,我们可以更好地理解和应用这些概念,为我们的学习和工作带来更多的便利。